La numérotation binaire et décimale

Avant de parler IP, il est indispensable de parler binaire. En effet, si je vous donne l'IP actuelle de mon ordinateur, 192.168.1.9, vous la voyez ainsi, car vous êtes un humain, mais en réalité, mon ordinateur la voit de cette manière : 11000000.10101000.00000001.00001001

C'est beaucoup moins facile à retenir et à manipuler pour un humain, non ? Pour un ordinateur en revanche, c'est le top, car il n'y a que 2 chiffres : 0 et 1. C'est le système binaire.

I. Principe de position

Dans notre système numérique « humain », nous comptons en base 10, appelé également le système décimal. Ce système, comme tout système numérique, comporte N chiffres allant de 0 à N-1 ; soit dans notre cas 10 chiffres allant de 0 à 9 (car oui, le zéro compte !).

Afin de continuer à compter au-delà des unités, nous utilisons un système de position des chiffres. Une fois les unités épuisées, nous ajoutons une position supplémentaire (dizaine) nous permettant de signifier le passage à un autre niveau.

Prenons le nombre décimal 5469, il est composé de :

• 9 unités
• 6 dizaines
• 4 centaines
• 5 milliers

Par décomposition, nous pouvons écrire :

• 5469 = (5 x 1000) + (4 x 100) + (6 x 10) + (9 x 1)

Ou encore :

• 5469 = (5x10³) + (4 x 10²) + (6 x 10¹) + (9 x 10⁰)

Dans ce dernier exemple, 10 représente la base (car nous sommes en base 10) et la puissance représente la position du chiffre composant le nombre :

Bien entendu, ces opérations, nous les faisons de manière automatique sans même se poser la question ni se rendre compte que nous les faisons, mais la compréhension de cette mécanique est très importante pour la suite.

II. le "2" n'existe pas !

Nous humains, comme cité plus haut, comptons en base 10 pour la simple et bonne raison que… nous avons dix doigts !

Pour ceux que ça intéresse, les gaulois avaient un système en base 20, car si on compte les orteils de pied... On appelle cela le système vicésimal et on en conserve quelques traces dans notre langue (quatre-vingts, quatre-vingt-dix).

Nous allons donc essayer de comprendre comment calcule un ordinateur, car c’est le fondement de la compréhension du réseau (et de bien d’autres domaines de l’informatique), notamment de l’adressage IP.

Ce système ne diffère en rien du précédent, en effet, il s’agit là encore d’un système à position, mais au lieu d’utiliser 10 chiffres, nous n’en utiliserons que 2 :

• 0 et 1

Oui, c'est tout ! Ces chiffres, que nous nommons bits (pour Binary Digit), sont l’unique base du système binaire, mais permettent de coder l’ensemble des chiffres de base 10.

Tout d’abord, revenons sur ce principe de position. Comme nous l’avons dit, une fois que les unités sont épuisées, nous ajoutons un chiffre à la position supérieure, exemple ici en base 10 avec 9+1 :

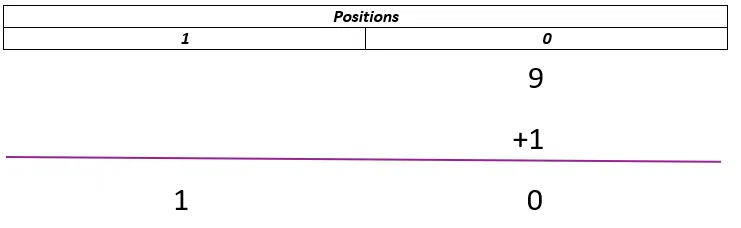
Et, c'est strictement identique en système binaire ! Si je commence à compter en binaire, cela donne ça :

Là, je n’ai plus rien à ajouter au niveau des unités, donc j’ajoute une unité à la position 1 :

Puis, je passe à l’unité suivante :

Encore une fois, je n’ai pas de chiffre après le « 1 » donc je passe à la position suivante :

Et ainsi de suite… Voilà, vous savez compter en binaire ! Mais, pour l’instant, ça ne veut pas dire grand-chose…

III. Conversion décimal vers binaire

Comme nous l’avons indiqué, le système binaire est un système à position. Tout comme le système décimal, chaque position équivaut, la valeur N^p ou « p » est la position concernée. Nous pouvons ainsi écrire une table des valeurs binaires en fonction de leur position avec les puissances de 2 :

Où la première ligne représente la position et la deuxième la valeur de "2 puissance la position" (2³ = 8, 2⁷=128, etc.)

Note : tout nombre à la puissance 0 est égal à 1 !

Il suffit donc de faire ensuite une série de soustractions, prenons 516, que nous allons chercher à convertir en binaire.

Premier constat, 516 est supérieur à 512, je soustrais donc :

516 – 512 = 4, comme j’ai utilisé la valeur « 512 », je mets un « 1 » à la case correspondante :

4 est inférieur à 256, je ne fais rien et je mets « 0 » à la valeur

4 est inférieur à 128, je ne fais rien et je mets « 0 » à la valeur

Je ne détaille pas, vous avez compris le principe, 4 étant inférieur aux quatre autres valeurs, on inscrit "0" :

Attention à ne pas confondre valeur de puissance et nombre de la position, beaucoup de débutants font cette erreur ! Ici, il ne faut pas mettre "1" à la position 4, car elle est égale à 16 !

Ah, là ça devient intéressant, car 4 est égal à 4 ! 4 – 4 = 0 et je mets « 1 » à la valeur :

Comme j’arrive à « 0 », je sais que je n’aurai plus de valeur à soustraire, car mon stock est vide, donc je mets 0 dans les cases restantes :

Et, nous avons notre nombre 516 au format binaire : 1000000100 !

IV. Conversion binaire vers décimal

Cette méthode de la position est également utile si on souhaite faire l’opération inverse. En effet, maintenant que l’on connaît les valeurs de chaque puissance de 2, il suffit de les additionner pour retrouver la valeur décimale d’un nombre binaire.

Exemple : prenons le nombre binaire 1010011, nous pouvons remplir notre tableau (en commençant par la droite) :

Si j’additionne les valeurs correspondantes aux Bits à « 1 », voici ce que j’obtiens : 64 + 16 + 2 + 1 = 83.

Et, voilà, nous avons réalisé une conversion binaire /décimale ! Facile, non ? Direction le prochain chapitre pour découvrir les adresses IP et leur structure.